Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
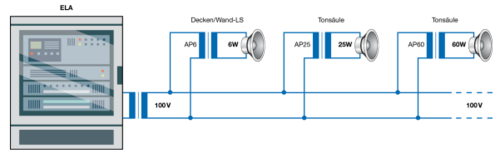
4.3 Vorteile von 100V-Lautsprechern
Der Vorteil der 100V-Technik liegt in der wirtschaftlichen Verkabelung der Anlagen
- Es können nahezu beliebig viele Lautsprecher verschiedenen Typs parallel angeschlossen werden
- Unterschiedliche Lautsprecherleistungen können an einen Verstärker angeschlossen werden
- Bei der Berechnung des Verstärkers brauchen nur die einzelnen Werte der Lautsprecher addiert aus dem Ergebnis ergibt sich die erforderliche Verstärkerleistung.
- Höhere Spannungen bedeuten geringere Ströme und damit geringere Leitungsquerschnitte. Gemäß VDE 0833-4 / 6.2.7.1 mindestens 0,8 mm Leiterdurchmesser.
- Durch Anpassung des Übertragers kann die vor Ort gewünschte Lautstärke erzeugt werden.
- Im Gegensatz zur niederohmigen Technik können Lautsprecher nicht überlastet werden.
Mathematische Grundlagen
Umrechnung Impedanz ↔ Leistung
{{data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAaAAAADQCAYAAABBY7UsAAAgAElEQVR4nO3dd3xTZd/H8StJB5S9ZAnIlKGgIAgyBAQZ3oJ73eLe2xtUFPBREfdGcIGoIHsPQUA2toUyuqB0b7p3mzZN8nn+SJO2NIWWtqQJv/frdf3TpMk5ycn5nmsehRBCCOEAytEbIIQQ4vIkASSEEMIhJICEEEI4hASQEEIIh5AAEkII4RASQEIIIRxCAkgIUQOFRB5Yz5o1ayxl3W5OZ5stD5lSOL51re2xdfsj0Dt2Y0U9IwEkhKgBA3H7P2dKRy1K05yRb20hNK/kIXM6J5Y9zyAvhbbjf/jknxiKHLqtor6RABJC1FAWf9zuiXIfyhfhpvIPFR/hrV46PKcsJdsxGyfqMQkgIUQN5fLnVE+U+3C+jjw3gI4ys7cOz6l/kuuYjRP1mASQEKKGJIDExZEAEkLUkASQuDgSQEKIGpIAEhdHAkgIUUNVCKA7lksAiQokgIR9BaH8s2oFK1asYMWK1eyPqmQArTkD/79WlTxvJRuOnMVk/5nVUqzPIzc3107JIy+/AL3BiLlKr2Qm9fASPvv4Uxbuiq24bfqzhJw8wYkTJzhxMpCY7Kq9qihLz5p7G9ofBWfwZnp3HY3uXydzgEQFEkDCLlPsfG52VyilUMqD237LsH/CL7nCtTxPQ+snd9R8roc5iZ/Ge5S8ZuVF16A5HXsPY8qLX7MzurCyPSH8y2G4Kx193jlG8bmbf3IO1+isr9mcaVsqex1ROQPe07uj1XbipX3nfPtZy7mzkRvXzDlZ4bMXQgJI2OUMAVS2aFqO5vPjBaUvkfoXn83+lUMJhWQtm0oD5cHYhQmYitPw3/gj6wINls13kgDK3TubYe3cS/e3WV+mLQ3H6OgNK1Ho8xZ93LW0v/t3Im0HQC7HPryJxo2H8+Xp+rKloj6RABJ21asAatiGLt260a2kdO16FZ07tMJLVz6EPAd/TLARwEzSr5NppBTKqxvjJw2kqaYBA+97iluu8kKjtPSY4Y2BugggM2krn2PiM1+wMSijVgPCcGwW/XQKpZpy94pKvg+HKeDUH89yU4cGNGzXj5vGjOGmvu25ovd/eHdHfL0JSlG/SAAJu+pTAHmM/4kkO29elPgPbw9rUhpCbv15P8AImIjb+QUv3Teaa9p7oS3bbOfVll5DbuXBT/aSYa6bAEpZNAEPpVCaxnS75Tm+2nyKzNo4A2cvY4qnQul68daRetqgZS4kPeYMwUGnCE/MkWY3cV4SQMKumgeQkdAf7mFg//70r1K5nru+P225Uq5iAAHkrbufpqo0QB7ZWj5A8v2/4pZWGsvjntfyv72Z5fajTgPIVjQ07j6eF77eyumsGgzRyFvBnZ4KpevD235yahfOTwJI2FXzACrG/73+6Krcj6Oj76ySQQLVCKDMP++wNLUphdJ25pUDBttj+lM/MaWDDqXrxpOfvkJ/D4WmzUQWBJeGTF30ARWFrmf2Q8O4soGdvqomPZnw0rf8dSa7+qMFJYCEi5EAEnbV9wAyG7KJ+fdHHupZ+jzNFdPYZFvxMoe9b1xLI6Wl/UPrSDHlsOelHuiUJz2e+4uMktery0EIxenBbJ3/OncMaIP7ufurbUqvSS8zf0coOVXtzLnIADIW5JCVmUlmNUtWjl76bkSdkgASdtVGH1B+XAA+3t54V6n44B+Xb/nHcwch6Dzw8vKylYae7uX6dZRSKE1Lbl14pnyfgzmLY4vnszXBUtcwp+/njz9PkFlmRy7NKLhCzvqt4bPnJnB1M905wevJhEXJVRtQcFEBZODgq10qfl5VKNoeM/A2XPgdhLhYEkDCrosNoDYOGIbt0f4mnl3iT+5FDAu71MOwTSkH+HhiR9xU6Wd7y49n6zCATMTunM+8uXOZW80yb+Fu4mtjVrEQlZAAEnaZ4hcwpkwATV6SXkkAHeGtq0sDqO0zO20BVJgcRlBgIIFVKkGEJZfMlT8ngDRNOtP/+gH06dqaBpoy4ePZnft/8COtBlfpFxNA5oyl3NnCq1ytzFKaM/GnBDt9OwZSTm7gyxcn0afFuTUgD8b/nFSHAVS3qlurshYhQAJIVMKcupiJHlU4SRr+5X/dtCXP09LppX2UTPGsgz4gE+l+33Nn5zIn8cYDeGmLvZN+1VxUAKUvYZKHvX1wZ/T3cbZtMWWHsevnt7hvcHs8Kzy3IZ1vfpJP1weQXtWOlnoYQELUhASQsK9gHfc3sp4s3bjh49P2O6SLtvNEa40tREqXu6m7QQj5vrMZ2LDM/zYexkcnLm6lsboIIH3EVj56YjRdG2sqPqfBlQx/7CPWnEit/hyZiwogM7mxAfgdPcrRaha/wDjy6tdsV+FiJICEfcW+vNGztKbRcPR8zl3oGMB46iMGuZWegMcsTCipKRkJ+XYyvcqsYHD+0osJXwVXcR6QnuMf3EDDMif2BtfP4WhBxe274G5eTB9QUST7V1sXai1bVrMnLN/OPCCFZ4ehPPzBCvySa9BeKIMQhIuRABKVyGHDQy3RWE9ImmYMeXUtp7OtKWSmIGobb93UvPQ5tTVDvyrzgPTHeH9Qg3JNWoPn+Vd7AETdTkT1oO3gB3l3mS9nazwyg4uuAaX4bWDZ0qUsrWb5c9NxUqUGJOqQBJColP7ILPp7lr8q1ni04MqevenVpTUNteUfazzqG0JrY+JIFSei6o/O4fqy29dkNN+FVW8D6iKAUn+fxtD73uG3w/G1ewsC21I8V9ffpXiEqAYJIHEehZxedDdX2e3vKF8a9HyY5ZG1dFKs8koIBfjOGlCmg19Dq9t/I64aIxKcZTVsgGL/9+jvZtnOe1dlOnpzhKgxCSBxASYyjv/BzHuH0q25+znB406L7sN5cM5KArNqsa2mGkvxkO/DzGvLzBnSduC/61OrvFK0swRQ7r53GdHRs7Qm2qwf0/6oP7djEOJiSACJajCSn36W2KhIIqPjSc2tq2YgI9kJ4YSFhREWFkZ4QvZ5T7SGjDjCS54bFhZORFJePbtVgWszZwWzc90a1qyxlrWsXb+Z7fuOEZEhoxhE5SSAhBA1Ys4NYeOMETTXKLRdRvPoU0/x5MN3MqpnM3TubRn28jqipctK2CEBJISoMVP4Fwx1V3jevQrbaHhDNL/d0QaNasqU36u42oO4rEgACSFqzBT5NcPPDSAgf/U9eCktnV/ejzTGiXNJAAkhasx+AJlJ/+02PJU7Qz49IwMmRAUSQEKIGrMXQMXJe3nzBi88ejzJ5mRpgBMVSQAJIWrMGkDaNtcweuxoRtxwNVd4deDm13/lSKrc00HYJwEkhKgxawB5jP8Cv0B/fDfO4uaWbrQa9hY7pfYjKiEBJISosYpNcEbCvruZRkrDFXctI0EqQcIOCSAhRI3ZHYRQ4M2bfd1Q2s48+VemDMMWFUgACSFqzBjyCYPdFB6Tl5BuSxoz6Run0UGrcLv6FfbW5nJNwiVIAAkhasQUt44XB7W23HywQWdGf7CPnNIH+eOONmiUhuYDHuX3EBmMLUpJAAkhhHAICSAhhBAOIQEkhBDCISSAhBBCOIQEkBBCCIeQABJCCOEQEkBCCCEcQgJICCGEQ0gACSHEZciUn0SI37/8eyKSTAfdMl0CSAghLismIhdN5ao+U3jn+x/48L7etL5+FofyL/2WSAAJIcRlxUyqz0o2BVmWjTXFL2CM13V8EHjpl0mSABLCVRiiObR+DWvWWMq6ncFY1/80p57kr7XWx9axL8wBl7uibpiSOLZlre17X7NmHfvDreHiwwbr9752I74V7othIm7JFK4cPJfjRZd+0yWAhHAVxfEc/PouOmsVqslNTN8YQq41gDL9WfHSEBorLe0nfciuqELHbquoPeY0fD+fRFuNQimF53UvsiXKkiams/uYNbKZZTHY0e9xMLlsAJlJ2/MmI4c+y4Y4xywSKwEkhCvJX8mdngq3QR9x+pxzSvGJ2fTTeTDp1zS5N4+LMacsYoKHQiktPWZ4Y7A9YiT0syG4KXdu+jKC0vgxk77vHcaNf5s9qY47GiSAhHAlhWu4x1PhNuRTzpwbQCfncI3Og9t+y5AAcjHm9CVM8lAopaPXW0coHdRmIvyLobgrd0Z8E2ULIGPEL/znminM/zeUsLBT7P3iOT72Nth/8TokASSEK5EAuixVL4AMHPl4AjcMHMhAaxk8lW8CLv1YbAkgIVyJBNBlqbo1oPpCAkgIVyIBdFmSABJCOF4VA0i4lqoFULQEUCkzxfo8cnNzy5W8vHzyCwopKq6ra7Q8QnavYsWKFaxYsYLVB2Ow3/JpJu3EVlaWPG/lJj+SK3x7ZnKO/clnH3/C11vDqTCQUX+WkJMnOHHiBCdOBhKTLdedoo4VbuShJpWMgjs6k966Bty1SuYAuZycP5nqaRkF1316+VFwIR/fgJvyYNyPZ+tdzddxAWSKZ8EYd5RSlRatZ1Pa9hjClFd/4FBSLY1TN0Xw5U2l7+s59U9y7T7RwL/Tu6MteZ6m/XP8U2GilpnUxRPxUFo6vrCHc8eQWK44rfvTnGlbZO6FqGPFfrzdW4em/bPsOudwy1lzH03dejPzqIMW/hJ1x3CAVzprUUrR7KENlF5iGDjwShe0mtY8tk3vwA20r14HUNni1vkefguvhWGCtRFAOfv49u0f+Ce6AP3WR2iu3Bj00WmMpixO//UTK/0sX78EUNXk7p3NsHZ2jgWNDs8mbelxw0Qef38l/pn15PrNnMmumTdyhZt1W3W0uu5Z1sSWqSIXB/LDHT1pXDI5UHm0Y9jbu6j7XTDgN/taPLRXMGVROLYjLu8kn45qiteNnxAk+VOJHDZMuwJdZechrQeNWnai7/CpPPfxGgIy61ODViFHZ/fHUyk0rSax8IzlmzcmrueRLlp0XZ7l7xwHb6Id9SeAvNpwVbdudOvWlas6d+SKZp62k7+1NB4zn/Cafue1EEDZ6x+kpUahPK9k1G030kbjRr87n2ZSryZolIZ2T+1AjwRQdRiOzaKfTqF0fXjzUCb5BQXkpsXg//dCnrmhORqlaNDnBf5KqSchRCEHXumKVik0VzzCFnsHkTmZXyd5oZSOPjOPcMlWOtGHsPzFEXRs2JC2fYcyesxN9Gvfhl6TZ7E19tLP9XAqphTWPtgWjS102nPbnF/4ddGPfDXnSW7u5GE7d7hfdR9/RNSjNC+KYvOs2+nX0g3l0YJO3bvQ2qsRnUc+y5IA+2c5R6s3AeQxcTHlJ+QWknjoW+7s4lYaQm4Dar5gXo0DyEzywQW8/uA4BlzZuNzVkrZha7oPuoX75mwj0SQBVC3Zy5jiqVC6a5hzsvyP2pyyhgfaalBKR++3j1bSZ3epmYj5bhTuSuF23QfYPywN7HvxSrTKg4mLUy95+7u5MIPYM8EEnQonMad+fGr1n4nwL4fhbv1d6/rwtl/pZ2eM/pmJzTQlv2kNLe5ajgMXErDPVEhGYjSRUXGk5Nbv770eBxCAmcw199HC2oyhGnDnilzASOgP9zCwf3/6V6lcz13fn7YMEqjFPqCi0EVMba8tCcfuPLkludxJxvEBVIPP6VLLW8GdlQQQFLDlkVZolMJ9xNdE1YuWDxNx34+2BNDAeZyqJIAOvtoFrZKhz5DPX68NruJx2J/+A4bwxm4HrI6JiahvRlQaQJDJsqletvOHpsWjbJXryotWzwMIio+8xdW2k7gHExalYKYY//f6V95WW6Ho6DvrmOXKuZYCyBC1nIe6uqO0Hbj/o7e4yUuhaTaCeUfzSrfd4QFUg8/pUjtvABVz5K1e6JTCbUBltY1LrY4DyJxK4D9/s/90posEVy5/TvWscp+vUg24d60jzuwXCqAidj/bvrSJzvNOVuRV+mLiAup5ABXiP/cGPGwHZQse2aKnRifWWgkgPUc/vJFmGg0tb/uVGJOeo7P646Hc6PjAShJLrtAlgKrhvAFUxK5n2qFRioa3/UbaBc/IZoryssjMzKx2ycqvah9JHQeQ4SCvdvHg2ndP1pMmx5pylQDSs+nhZqXN7p1eYl8VDhljQQ5ZF3M85ugd0yJxidSbAHIf/h57j1vmzBz38+HA32tY8PpYOrqVOSibTmVpSSd0flwAPt7eeFep+OAfVzIwsdaa4PII/vMb1kaUHB45viz/3ZvUMkeL4wOoBp/TpXa+AMrfz6vdtSjVlNuWJF74RF7NEZZlS+XHQ4U3qf0AKg5l5WeLOZZpBmMInwz2YuwPiZgxkXp4AV9ujKt3EwmrzkTaGd8qHofeePscITTdEXW/CwSQ/iCvdS9pdldaOj23iwv/YqzHQfWPR22PGThgjdBLpt4E0IWLFzd+dJIan8JNEXx1MQHUwd48oPOrDwHkNOwGkJn82H18c3dX3JWWNhMXcrpKP8Yc/JZ+xNy5c6tdPl4TVGE+l321H0BFxz9mWHMtnl1v55O9p1h0WyseWHmG7XPG0cHdjTYTfyDMlS+H64VKAshYQOqZf5j/YC88Sx5z6/wQq+OrcklgInbnfOZdxPE4b+FuqvQWTso5AsitDcPf3E5imR9fYXIYQYGBBFapBBGWXDIJyxTFNyPKBNCUZdgfHm/g8P+62QJIe+WL7K3mlUh9CKCL/pwuNWsAKU/adO9L37696d6xOR4aHU2uGs60T7YTXa/yu26a4EyZwWz89HFu6tyRtq0b0aZte7qOeY5vdoTZbi5nz8XU9qzl0jCTFRtcxeMwkMCgYGIdsnLIOQFk93zUgn53vs9fMY4YJFFRTb57xx4T9SiANK36MHLsWMbecgvjxt/KxP/cwX3TnmX6vF/461TmOU0PNejbMCfywy2lY/k9Ji/Bfk3fwP6XO5UGULfXOex0AeSMfUC9eGG9PwH+JwkIDiUmtaCeNjvVVR+QgeSjy5g1pReNtVp0za/h/g/XEpDh7FUfJ+0D0l7JnZ/8yfI/l/HnynVs3XOU8HQXbhO7xOpNAFU2Cs6+mpxY81h5V0PbY+7DvqhkcmshW6Y1tz1P1/89/Kt5DpAAqobzDkKoLgMpZ45x9OjRapdj4elVDDwT8QvGXDCALBcxnvznj6wLvmJx2GpeG9+NRp6dmPD+ej7/Tzvun7+aN0e1xb1pb26f/Rdx9TONq8BJA6jCIISLYSY3NgC/izge/QLjyHONYZB2OWkAGQn5djK9unWjW5VKLyZ8FVwymsTAodeuKu0QbDSOH2Pt/KqLA3h/QOkkWI9bfyG5mgeC4wOoJp/TJVabAXRJBiGYyfhtMh5K4TbgfQLsfmhF7HiyDRrVmAc3XPi7N2fu4JXx9/ONdxomUyRfDW9smcBafJa9H9/BpFmHq9DhXV/ls/m5PlU8DrvRrXs/Xt5RH+cBXQwZhFAZJw2gmslcdS/NbV+yhubDprPhTI7tytecH8Hm6TfS1DYBVke/2SeqXTNwfAA5kVqtARVwZtdyli5dWu2yfH9Ulb/non+ep4PmPANUzKksmuBxcSt4FPvwRk9PBs475dLDcOufuqkBpfhtYNlFHI9/bjpe/1ZaqEWXZQBR8C9v9vMof7Wh8aRFp55c3bMzrRpoyj/W5BYWRFS/7UMCqBpsS/E40WrNWet5qLUGpevNm74Vv1tz0lKmNtfgdu0cTlR3l4whrH73DT7eXP/u4eLaTIR/UXYpnl686eskx6MTujwDCNAH/cjUTlVopml4NY+vjrmoq1AJoKor9n+P/m4KpRox8ZcqzPWpFwyEfD+OlhpFw2ufYXlwli0sihL2Mm/8FWg9+/LyrnQn2R+BOY11D5VZjFQ15tYfL+73Ly7ssg0gAFOaH7+9cTc3XtUMt3OCx6NFT0Y+/D5rgnMu+uQhAVQ1ufveZUTHMh3Ujboyds7uS3Drglpgzubkkpe4pUcz3JQ7TdtfRbcuV9DYoyndxzzLgn9TpAbjNHLZ9FjbCucCpW3MNe8cruL8MFEdDrwjqpHshHDCwsIICwsjPDHHoT9UY346ibFRREZGk5Ca5yLLn4hLx0h+ShQhgQEEhUSRnOeIa2Yz6QHbWbtmDWtKytq169iwZQcHjkeTJQf15UEfwYH1pceA9TjYuPUffM6kXrrbglSBAwNICFG7zGQFruLlwY1QyoPu4x7lqaee4L9TR9CtiRaPDqOYsTVeamSuriiarS9dTwOlUEpLuyF38cA9k7ihQwOUcqPVoKdZHlY/YkgCSAiXYiTg/QG4ndPkWxS6gAnNNWhaPcBap2jbFDVRfOQteukUpXcQAHPGDp7palnHrvH4n7A3++RSkwASwqUYCf7w+goBhDmD3yZ7oHRXO88oQ3HRiv3eps85AQRFbH+itWWARYtH2VoPKkESQEK4lMoCKIGFY9xRnqOZH1MPLn1FnbIfQHo2l6zuUl8muEoACeFS7AWQgYTtL3OtZwP6vLyTDGmBc3n2Aqg4bjn3d9CiNM0Y/c2pejHQSgJICJdiDSA32vUfw9jRwxnUsxVencbx5tITZEjl57JQGkAaWvYZyZiRA+ncRIuu/c38b1kADllo3A4JICFcijWAmnD798cJ9PdmzYyhNHVry83v7a9k5XfhakoDyI3BM9axZeGj9PFUKF0bbv7wMFn15DiQABLCpdhpgisO4uMhDVDajjy8PkVWZbgMVGyCy2X38yULoup68OqB+rGsrQSQEC7F/iCE3D0v0V2n0PV4hX1VW+5bODF7fUDGkE8Z4mFZ3aHJpEX14k6rEkBCuJRiTszuh055cc/qvNI/m5NYfndrNMqT/jO9yav8BYQLMBx8jau0CqXcuXl+rGXysTmNtQ9eYRmGrevBi3uyHb2ZEkBCuA4jEX8+Qf+WlsmGXt1u5TPv0lusGyN+5NYWGpS2NTc8t4rIenAFLGqfOfsfZg5sYVtQ1f3KSSwMtIx5Kw75mpGNS+411GoIc/Y7tjosASSEEMIhJICEEEI4hASQEEIIh5AAEkII4RASQEIIIRxCAkgIIYRDSAAJIYRwCAkgIYQQDiEBJIQQwiEkgIQQQjiEBJAQQgiHkAASQgjhEBJAQgghHEICSAghhENIAAkhhHAICSAhhBAOIQEkhBDCISSAhBBCOIQEkBBCCIeQABJCCOEQEkBCCCEcQgJICCGEQ0gACSGEcAgJICGEEA4hASSEEMIhJICEcICT7QdwrGFXKVJcppxsP6DavwMJICEc4FjDro7eBCFq1cUc0xJAQjiABJBwNRJAQjgJCSDhaiSAhHASEkDC1UgACeEkJICEq5EAEsJJSAAJVyMBJISTkAASrkYCSAgnIQEkXI0EkBBOQgJIuBoJICGchASQcDUSQEI4CQkg4WokgIRwEhJAwtVIAAnhJCSAhKuRABLCSUgACVcjASSEk5AAErXNbDZXWqry3JqSABLCSUgAOU5tnXgv9nUu5v/OFxhmsxmTyURxcTFFRUUUFhbaSlFREcXFxbbnm81mjEaj3ecZjcYafR4SQEI4CQmgmrOeeA0GAwaDAZPJVOkJ1HrStp589Xo9er3+ok68575OYWEhBoPhvK9jfX9rSJT9vwttt3UfCwsLbdtcXFxs+z+z2UxRURGpqalER0cTHh5OeHg4ERERxMbGkpmZaQsho9FITk4O8fHxRERElHteVlZWubCqLgkgIZyEBNDFs56Ui4qKyMzMJDo0mPC4JAoKCiptbjKZTBQUFJCSHE+A7wH+3rkP34DTREdHk5aWhl6vP28QlH2dwsJC0tPTiQj2Y+/u3Rw4EkR0bCzp6ekUFhZWeB3riT8/P5/kxGiOH97Lzj2H8A+JID4+nqysLAwGQ4X3tgZWTk4OMWdOsn/PHvYfCSQ8MpKkpCTy8vIwGo2YTEX4fjCYxhqFUqVF27Add3yxh/j4eIqKijCbzWRuepbOjbTln9d0GO9u9SYhIcH2vIshASSEk5AAqr6ytYHs7GyiA3fy0WMj6NCwLQ8s8iUjIwOj0Wj3f/JyE9j26TQGtfdCq9Gi0yqUeyt6j3+Rn3d4ExMTQ0FBASaTqdL3t4RYPqd3f8dDQzvRSKdBp9OilDsteo7l5R+2Ex0XV+51rOGTnX6GZW/eTu9WHiitDp1GoW3YgUF3z2K9jz8pKSnlTv5msxmDoYiYQz/xyE2dK7zX899uJDgkxFZrKSrKw/e722itLQmWBv154ZfVHD9+nPT09HI1oMzwJUxsqUEphXvniXy4bCMBAQFkZGRIDUiIy4EEUPVYT555eXkkRvmxeOYdXN285Epe244Hf9hDSkqK3QDS69PZ+tZgGms86DR+Bsv+PkSQ3198cW9PPJXCs+vdLPj74HlrANZmrsh/PuCG5hrc2t3Mm79u40TAEbZ+8196NVQo907c++0OEhITbTUas9lMfl4Uix7sjrumMf3u/5BNB304eXAVM26+Aq3S0HTgC2w4ctwWoNZ9Tf73E4a20ODWfjSv/7ieo8e92f7dNK4uea87PlnL6ZAQW02oIDeAt67zQCmFptFwZq3aQEhISLmaodlspihvP8900aK07Zjw7h8cOnSIpKQku7Ww6pAAEsJJSABVj7UWs2P+Cwzv1JAGbftwXa/WuCmF0nbgvz/9YzeAjEYjyYffpZ+nQttmIl9u30tsbCx5eXlkJGxnWhcdSrnTa9p8jp08SU5Ojt1akMlkIivjBG/e4IXStOTWuZuIiIwkOzub9PSzrHy6B1qlcLvqPlYfDyA3N9c2MCB89aO01yrcej3KigOHSUxMJCcnh8TABYxuokFpmjJy5krCIyIoLCzEbDZTWHCK/xvaCKVpyS1zVnLi5EnS0tLIyUljy0tXo1UKXZd7WPzPfs6ePUtxcTFGo4Hj84bhXvKZ3PnpKoKCgsjPzy8XQPmBH9LfTeHe50l+3ryVM2fOVNp8WR0SQEI4CQmg6jGZTGSGLWJCpz7cNuNn9hwP5MSudxjgplDajnYDyFJryWXNE53QKg0tJ/wfPsePk52dXdKUV8Dm57qiVQptp7tY9M8+kpOT7daiiouLidnxCp21Ck2Tm/nywBEyMzMxGo0YDAtRviUAAB+ASURBVAaid02nm06hNG25b+E/JCcnU1xcjL4gni/GN0YpHb0eXUjgqVPk5+eXNOcl8e2kJiil8Lz+BXb5HSM7Oxuj0Uj6/ul01Sk0TUbz/ua/iYmJsQ2YSD/8Nj1L3mvqp+sIDQ219WHlBH/GIHeFUlo63/Mph318yMzMtIWqyWTAZ9a1uKlGDH71N/YfOEBSUlKNmt6sJICEcBISQNVjaUorICE+keTkZLKysoj3/5wb3EsDKDU1tUIA5Wfv54mrdCjlxoDnl3A6JAS9Xm9r5opZcgdeSqF0fXnhj61ER0dXaIqyvHceW17tjU4p3K5+jO0BpTULk8lEWsJKbmuuQSkdVz/xC5ElgZGd8Ae3NlIoTVNunbu53OsbDIUcmjPIUotrNJJPdh8gNTUVg0HP/rf6oVMK3dWPsGLvflu4ms1mCjI3cFcLy3v1ePhb/E6csNW4ivQhvDvY0gyn63ofi//eRUJCgi1givMP8UI3HZqWE5izagsBAZbamswDEuIyIgFUPWXnulhLcvBXDL5AAGVHL2S4h0KphoyZvZ6IiAhbP4/JZCJ972t00SmUpjW3zVtLaGiorRms7Ovk5SXx2bgGKKXwGDqdk2WeZzKZyM7w4bleOpTS0HTcuwSHhlJQUEDSvhmWmpH2Sh5auL1cGBiNRqKX3ElDpVC6Xjy39G8SExPR61NZMLmhZZDA4FfY4+1tq8WYzWaKCk7wv75uKKWhyeiZHCjzuNFowO/DGy3NcLqePPbDes6cOWML3fRtT9FOq6X9nV/w165dtpqVBJAQlxEJoJoxGo0XDCCTyUSazxyu1imUpgWT5m201UCgJKD859HfzRJQo95exenTpyv0h5jNZnKyApl+nRtKKRqNncPpMkFmNpvJyw1n1hB3S2jc+D/8Tp0iLy+PuFX/pYVGoXTdeeb3XSQlJdlqMiaTibObnuQKrSWgHvh+K7GxseTnnmLODZbXajTqTQ4dOWJrNgQoNsTy0XCPkoB6mZ0HD5Kenm4LqOyAT7jeXaGUG30e/Z4jfn4lTXsZLLu3FRrd1Tz8/UaOHDlCRkbGeUf+VYcEkKsz53JmzzrWrFlTUtZzMKqo5EETyce3stb62NrN+CXVzoFVJ0wJ+G5YW7ov63YQkGH90ecRurfMfq7bR3iBQ7e21kkA1UxVAyhln6UvRWlacfsnm4iJiSkXQDlnvuIGN4VS7gybvoLg4OAKAWQymchKP8oLfSw1nCbj3iMkMpKioiLb6+TnxTF3hCU03Aa+yL9BweTm5hL92900KqnhPL9sd7k+JpPJRPLfL9JRa+nPueurzcTExJCXfZwZ15bWcP49epTs7GzbNhUbkvlqjCWA3K57lq37D5CWlmYLtiL9aWYPKgmovo+x+p+9JCUlURD7KxOaaGgw8DX+2Lbd1ndUG7UfkABynMI49s1/jVnr4qnslJ8XspFPnr+XSRNu477nP2L96Vy7zzOm+LB45qNMnTiRqdNm8MP+BAy2RwsI2/AqQ5pY2n+7PfADPonFJY+ZyQxey+tDGqGUOz0f/IGjqdU/sEyZ/qyY8xILjhVX9gzSjv7GO49PZeKEKTw8fQF744rsPvO8+2xK4vAXU7hSq1Ca5tw8axuhOdbt1ROz70umdtSiNK0ZM2s7UYXV3pV6TQKoZqoaQKnes0pqQM2YOG9ThRpQzukvGOSmUMqLm99exalTp+wHUEYAr/W31IC8Rs+yE0AxvDfcEkAeN76O36lTlgBa/iDNNQql68ZTv+2qGEDbn6dDSQ3owflbLCP0coKZNcjyWg1HzOBwhQA6y+ejS2tAfx8oH0BGo4Ej7w+29C159OflPzYTHh5K4JejaKBpxsiZK2t18IGVBNClZs4icOXbTO7uZbmC+jLCbgAVnvyMka26cM+PPkTHBbL6mX40aDaCzwPKn7jNKdt4plcLBr22kVPxURz66jbauXfm4XWJZV63kH+n90CnPBj341nKHzoG9r3UCbdOz/B3TjX3pTCWf75+lEGtdShNO57ZZS9UzKT//SJ9ml/HS+uCiIv2Zv7UDrhfeT8r48vveZX22RTHj+O8UNpu/O+wofxbmWKZf7MHjcYuIKoeV+QuVm0E0PkWn6zqopTOqqoBlB70OQPdFEp5MvLttUSWBIf188g69h593awjytaW6y8p+zrZWVHMuamkiW3wa5wIDy/fBJdzircGWmotLSd8QGBICPn5+cRttQZMe+5f8Ddnz54t3wS37hFaaiyDIF78czvx8fHk58Xy6c0lATPwBf7x9SUrK6u0Ca4onPdvdEcpDS3GzWbf4cPlmtJMJhPZ/vMsIwSVJ4NeXMyxo+uYOcAdbbu7mLd+G/7+/raBC7VFAuhSKjzCJ2P7M+rpL1n6+Z2017oz4puoigFkTmDx5CZ4jvyWaOuDWWu4v4WW5vesJN12nBs4MrM37m0fZ1teyZ+MIXx8gxu63jM5WqZCUuz3Nn10Glo8sI7ssu9VfILZ1zTgug8CKT+Q9PxMMct55PpB3DVnMUteug43TQee32MngIqPM+cad1o/vBFrvpnCv2CYu5bu0/8tralVeZ/NJC+ZTCPlxuBPzpTbZnPqH0xp2pZpm8rtocuoaQCVXRXg3IUlz11k0rp2mGXZFpNLhFFVAshsNpOTto4pJaPT+j75MyHnDB5I2/q0pQ/G/TpeW7GVqKgo23I6ZUtOTjqLH2yHRil03f/LtuDS0XRms5mcjD080lmHUjquefZXwiIi0Ov1pAR/aRmpp7wY83+biI+PLzcIIez7W/FQCk3zcXzx9x6SkpLQ63NY/VgHy1yfrvezbP+hcn08hoLDPNvVMrKv7+ML8Tmnj8gyjyiYt68vqUUNfpG1Cx+iq07HVQ8t5O/du2t18IGVBNClZM4jMT4DE2AMnMt1bvYDyJy6hMkNdfR8wwdbhpgTWDjWA03LR9mqL/lbsR9v99bhcesvpJQJpYOvXYXWbRAfnSpzei4+ysyrdWhaP8LmMq1aRYf/R4/GY1kYY++qJpPfb7+CaVvstGUZU4lLtPw9f+VdeFYSQMUn3+VanQdjFyaU1ryKfXijpw5d//fwN1ZznwFz0q9M8lK43/QVEbbNNhH3wzgad3+Ngy7W9GZV0wAymUwUxPmyfPEiFixYwPz588uV779fwIKFP/LTr0tZs3UvJ8JiSElJIScnh6Kioguue1bf2Qsge/OA8vOimDuyoaU/5eaZ+AYEkJeXZ2uqOvHRMNyUQtdrGn/s+se2GoJeryc3N5fc3FwKCgrIy8vF+4vxliHbDYfy2SF/2+uYTCbSz3zLEA+F0nXh0V/+tq2/lpV2kCe761BKS5f7v+VMmcELxcUFbHjaMkep0U2vs8vbm4yMDAyGIkJ+vM3Sd9RwCHO27Ck3eKEgZiEjPBRK15UHvl5DYGBghcmmRmMR3u8OtDTDeQ1kwqjWaD2u4Zlfan/wgZUEkIOcL4AM//6Pblp3hn9d9rEitj3aAo37KL6zhkXWUm5voGj+yBZKz7kmor8dibumJY/9VTYQDPi+2Qudpi1Pbrf2zuex4+mOtLpnJWllzysFPnz6xAzWhmay45mbeOPfdAJ/e5FnFgRzTqMXcP4Ayl15Fw1VYx7cUCYVSoJFNfkvmwqruc8A5rMsnuiF8hzNfOvfjWf47EYvrp8bVK2anDOpjQDKCl7Fs2O64nXOIpR2i3szug69m1m/7SYyNpbc3NwaL79/qVlrG9aFSOP/fZc+bgqluYK7v9lBYskSOOVXiS7k6Ne30lij0DQbwUfbD5KSkoLBYECfH8y7N3iiVCMGvvALvkePkpGRQUHsGl4YN5rhIyfz9lp/4uPjycnJIerkj4xprkFpGjHq/7aSmpZWsg6bnqOfjqKBUjTo9yRrD3uTnp5esgBpDhtf6YubUmg73c0KP39ycnIsS+ek7+SRzlqU9gomfrCSoKAg27I66RG/M6GF5b2GzfiT8JIaldFo4NS3Y2hY8l6/bttOVFRUhdqMyWQi8/gHXONm+f41SoPXDS+yfMtWQkuGiNf2dy8B5CDnC6Ci7U/QSuPB2B/K1BpK+mrK1mxMsfO52V1D26d3UnrqN5O6eCIeqgH3rtGXe12D7xv00mnp+Nxu9IA5cw33t+nEszvzy29AcQp+f87mvpGjGD2oP0PGjGD0tHmsC8q0219VeQCZOfvjODw0LXlsW9nHsvjjdk+U5x0sz63ePtted9EEvFQDxv1oeX7x8dlc0+QWFsa6YOdPidpogtPr9cTHBfHhuOZolGX2e/uJ77B6wyb27d/H3l1bWf7Tx7w45Vqa60qCSNuSYa//SlBoqK0PwFlCyGQyoc/LIi7qDEf2rmXOf66yXOErLVeMeI4lm3YTHBZFSnqWrRnNaDSSfvYQr17fBI3S0Xbky6z715+kuADWvjmcZhoNzQY9z5Ltu4iMjESv15MT8iVD3K1DtzcTGBhIZmYmqalnWf3mjTTRKLSthjJ7jTfJ6cmc+ut9RrTSoGncn6cXbip3gjcYDMQFr+SuLu4o1YCed8/lwOkoMuKP8/MjffBUbnQYP4v1e/YSHx9vm6RaUJDDjvdG0FSj0LYcwvQlfxN3No7Qvz9kdGsNmibX8fg3q/H19bWFXVlms5nC/ADe6G9phlOaFox5cxH79u2zDT6obRJADnLeANr5NG017oz8NqbMYwb2vtARrftwvoosabdN+IGxHhpaPratXAClLJqAh2pWsenM4MOMnjq0XV5mf5GZs79Opnnft/GzU60pTDjMr29MYUC7tlx54728u+IYqZUcf+cLIMu2NOG/m8puSya/3+aJavQA6wurt8+2V078mVsbKrwmLSbJXMiBV7rR+t5VZfqKXE9t9QHl5eWwa+ZA24n4yrs+xe/kSVJTU8nOziYjI4OEhBi2zxtHS+tKyR49eHbJLuLi4mq9H6CuWE7m+ax/wtI3cr7ansfojwhNTradzAsLC4nx38gr43vS1E2hNG64u2nQeF7BNVPeYNGWXQQHB9uWwckJ+ZLBbpbRmRM+2MDJkyfJysoiPz+fqMgAfvrfJHo2sww4cHN3Q6M8aNXnNl79fi3HSlafLjvQICcnB//dP/Dg4A401CqUzh13nULXuDND/zuXP7fvIiQkpNwFQXFxMWmpkSx9Zwo9m5/zXv1u59X5a9h/4AAxMTEVJs5aP6/i4kIOzroOnVJoO07hs1XrbIMP6uI7lwBykPMFUPGJOVyj09Fv9vHS/hD0bHyoCZom97PWOuAgfz0PNFF43v4HWaWvTNjnN+Km68fs4+cmhgHvGT3Qarvzv4Nn+HZUM4Z/FV6xVpO9jSf7DOTJJX5semk87+w6zPcP9OP6Gf9ir3vlfE1w+i3TaK48mLg4tbRmY4rimxHu6Hq9yZHiau6zlTmRn29tiGo8hT+itvJ4hy48v/ucmpyLqa1RcEVFhfh+ONwWQJ3u+YKgkhWQrR3oBoOBjLTjzChZKVkpLZ3u+oxjdXgyqm3W2kRycjLBwcH4+fnh4+PD4cOHOXToEIcPH8bHxwc/Pz+Cg4NJLhNA1nsBxcfH43fwL5Yt/pmff13O5t2H8PPzIzw83HZbA5PJhF6vJy4ujuPHj+Pn50d0dDT5+fkYjUZyc3OJjIzE5/A/rP7tJxYu/IWl63Zw4PBhgoKC7N5Wobi4mIyMDE6fPsWerStZtPB7fvx1OVt2H8DHx4fQ0FCysrLKNYlaV99OSkrC/9hh1v7xCwsX/swfa7ez98AB/Pz8iImJsa0rZ4/JZCI7LoDVy5ezcOkmDh0+XK6WVdskgBzkfAFE3iYebqWh0dRl2OZZGoP5cKAbnmO+x9bKZArny2HuaLtPx9tWi8lnyyOt0LV7ih12JmIavKfTQ6uj+39u59pWU/gj2d5BZaao0ADksfLuzjy5owgootD+1J3zBpAp5jtGeWjp8sqB0lqafgdPtdXR5tEt2HKlqvtcZhsTf76VhpomjJ56C62unU2FvHUxtRVABkMRfh+VD6Dgc4YSW05mBeyc3hddSS3BfeDz7Pz33zrpjK4L1iDR6/W2ml16enqFkpGRQXZ2tq0Jruz/FhUVkZOTQ2pqKklJSSQnJ5OZmUlBQYHt5G8dnZafn297j7y8PFs4WcMsLS2NuLg4oqKiiImJISkpiZycnPPeWC4vL4/k5GRiYmKIiooiNjaWlJQUW7jZ+7+ioiKys7NJTEwkOjqaqKgo4uPjSU9Pv+BN9KyhnZGRQWxsLGfPnrUFlgRQGaaIpUzr06ykHbts0eDWsAVX9h3BXS9/y85o/YVfzAFytj1BB42O3m/62qlV5LHnxa7oGo/huzDLWTXP+w36eXTg4Q1pZfpITMT+MpGmui48uS0dM2BKXMZdbRoy8P3j2M0LgzfTe2hRSkO7x7dx/qk/RcQf30dA8vlONsWEfDIEN9WUO5enU+EQNSXw2+0t0F35CBtTzYCZpFX3065Bf2YdLbvnVd3nUuaEnxjfUKFUA0Z9G1nphF5XcSkDCMBoLCboi1GWNcKUwq3f42zYt7/C0OWqvGdtlYvZX2uYXKjYew/r/xqNxgrD0it73rnPKRtS1iHw594iu7Jtt65lZ/2fsrfxvtj/q8pnZt3WC21jTTltAAGYM1dzXwsNSnkw6ZcE8goKyM9OIsx7DXOndsNTKTStxvCVf30Zl2vg0LzJjBzcizae1g7epnS5/ibG3P01ZRcSMOcc5du7r6Zl22u5ZdIoel/Zl3u+8SXr3OPAGM/WGaPo0KILQyeMZ9BVXbjppTVE2BuuVrIN/07vgVbXize8K6nSVIUxnN+fHMuw/p1obLujYlv63jiKW2dsKTeqznR2BzPHXEmLzkOYcOtguna+kedWhlUIyCrvs+0fEvhpfEM0ze/kz5T63yRUU5c+gAwcmze05HmKBje+zM6SGfRVqQFZr+LPN+eoOqXsaDVndbFheqn/r+z/1iWnDiCKTzLnGh1KeTJl2TnX8kXBfDLUshJtk8m/ctYpj1kz+vQYwsJiSL9AhhpzzxIRGkFizoXbocw5CZwJTST3kn4mRvKSIwmNSOT8m1j1fQbQp0RwJibD7vBwV3Opm+CKi/NY+fAVJa0MbvSa9jXevr7l7hVzvvcpKsri8LLPef/99/m///u/Gpb3+X6LP9klw5GFa3DuADIG8P4AN/sBhImor4dbmg+aP8LW+lIJEq7JFMmiBwbSv3//qpXrp/BNYPVOpJcqgGyj5WKXc3trjaV22/BaXvhlLcHBweUmMJ7vffJyI3mvZCmamhctVz26mOhqdIjXZtOflNprFi3LhQOopHNcKZTnnaw4dxSVELXJeIp5A92qfkLV9eQN3+qNmqizALr7cwJPnyYvL8/WR5EZtYu3R7axDF/WNKLftM/YuXcvCQkJVQoAs9lMbk48v7xyG6NGjWLEiBEMHz78osuIEaO4/71VRMfGXvD9z+0DqY3mPyn2l2yq6cRkFw4gM4k/jMVDKbRXvcbBKrTRGAtyyMrMJLOaJStH77Kz70UVOW0AaWje/z+89vrrvDtnFm+//iwPTLyBjl4lNZ8GHRj6+Eds+HsnoaGh5OXlVbn/p7CwkKSkJEJDQzl16lSNyunTp4mKirINPb7QexcVFZGWlkZsbCzR0dFS6qDEx8dXGApeXa4bQKYEfp3cFKW0dHv1ABceC2fg4KtdLjhhzV7R9phRZhi0uDzpSQj0wdvbu2rF5yQxedX70dZNACl0DZvRqkVzmjdrRrOWbWjfuSfXDhvHHY+/wddLN3Ho0CHCwsJsky6r2vxlnU+k1+spKCiocSksLKzS+5tMplpq9pNyvrJ//37bShASQGUCyJgZzLo3htNSo/Ds/Tx/VWmElInYnfOZN3cuc6tZ5i3cTbyrjwEWDldXTXAdp85l6/btHD58GG9vb3x8fDhy5AgnT54kLCyM5OTkSuedXOi9rEFUG6WqfQ4SQJemrF+/nqCgoCr1CVbGRQJIQ5OOvenbtw+9rrqCRjoNHq2vYfKriziaLskgLoVCUsODCAwMrFoJCiWpmndsrasAuvKuT/E9dozExETS0tJIT08nMzOT3Nxc9Hq97VYA1Q0faw2oNmo/BQUF5bblfCSALk3Zvn07ISUraFzmAeTB2M+OEOh/kpOBpwmPz7I/CdOBHH2wXK7lknHaPqDyS/FYJ1GWrXFczMnFbDZTqI/j20mtaNy4cS2UZlw3/S/SqtgHVFBQQFxcHEFBQfj7+0up5RIQEEBISIhtlfDLPIDsj4KrHjO5sQH4HT3K0WoWv8A4qtmcL1yNkweQvYmoNX2f3JwI/m9YLQ7DnvYLkbGxF1wM1Wy2zOS33p8nJydHSh2U3NzcGt8nSgLIRgYhiBowhrNwai+6detWtdLzFj496doBlJeXzZF9O/j999/55Zdf+Pnnny+6LFq0mPV/7a3ywpi13f8kpWb9cpWRALIxk+K3gWVLl7K0muXPTcdJlRqQqGO1F0CF+MwdVjoI4c7PCAoJqfUAMhgMpKWlER0dTURERI1KZGSk7SZvshKC63DuALItxePB5CV2FsIUwoXU3u0YCtg145qSVa41NL75bY6fOlXrd7w0m2t/LThnuyOrOD/nDqDs9TzUSmNpH35pL9UcVCSEU6mtG9LlxP3DM/08bE3ImibX88aq/aRnZFRplFl137O+LPtSH1xO+1oVThtApshlPHZNi9I+G10r+j/wE0FSOxcuqjYCKPff9xjQWFuxL1PrRc+nl5NWjcmmonqszZLnm5ir1+spLCys89sg1BdOG0CiDphSOL51LWvWrCkpa1m7bgNb/j6If2yOLDfkYDUNIJPJcqvnM2fOsH//frZt28bmzZvZsmULu3bt4tixYyQlJdXZ3S8vZ2azmWJDIj9PaWm7wV/5okHn0YhWV/bmxkmP8d7vB4jLyLTdJM9Vvw8JIFHKnM6JpU8zoIFCNbyaCY89xVNPPMSUoV3w0jSg0/g57LZ7B1VxKdRGDUiv15OSkkJMTAyRkZG2Tv6oqCgSEhKqtdyOqDrr+nRnEyNZ+UJ/ywAQTWOuu/8N/u+99/nwg9m88eKD3NK7ZcngEE+6TPmMI9GxtluluyIJIFFesS9v9NShaf8c/5TeQ5ugz0fRWGlo98RfyMLijlFbfUBl75RZtkgnf90yGo3k5OTg//PdNNMolKYFE95fha+vL6dPn+b06dMcO7qDd29pY7kHk6Y5Ez/ZXuUVyJ2RBJAor/goM3ufG0Bgil/AGHeF2/UfSj+bg9TGKDi4cEe4qBvWPqCIPx+iRUkA3fbxJiIjI8nLy6OgoIDMzExObXqBLlpLs1yb2z7kRGAgeXl5LvndSACJ8ioLoLDPGeqm8Jr8K9IK5xi1FUDCcYqLi4le+d/SAPpkM3FxcbYajtFoJD3kG250twRQszEzOeTrS1ZWlks2w0kAifLsBVBRDBue6oV7o+t460BNJ/yKiyUB5PyMRiMxKx+uEEDFxZZVMcxmM5neM+mpUyjlTp/HvsNbAqgcCSBXVhJAyqMj148Zy+ibrqdby0Z0nTyb1UHZMtnXgSSAnF9lAWStARUbUtnwVHd0SqFpNYq3fl1DQECANMGVIQHkyqw1oDb3seh4ICcPL+el671w73Arn/pIADmSBJDzKx9Azbjlnd/w9fXmdMBR9m34iTfv6E1jjaLBlaN59sul7N27l7i4uAsuwOqsJIBEeXaa4Ar9ZtPfXaG96hl2ZLrej8BZSAA5v3IBZHeV9I7c/OLX/LZ+M/v37yciIqLKt0F3RhJAojx7fUDmTLY90QmtcqffTN8q3N5c1AUJIOdXvgbUhBuf/ID5879j/ufvcN+A5miUQtd6EC/9uIWwsDDb4quuWPsBCSBxLsNhXu+mRdPiEbaUSRpT7CImNdegGg7hwxMSQY4gAeT8zu0DmvDeSry9vQkMDMRnxyfc3NKyTJK2zVjmHwwiOzvbZWs/IAEkyjKeZvGDfUsmyTWm53++5ZjtljUGTn01kiZKoWs7lNc2xuG6P4v6SQLI+VUYhFAyDygnJ4fU1GS2zhqKV8nSPFdMnod/RGSt3iajvpEAEsJJSAA5v/ONgjMYDCRGbWdat5I76+o68+jivaSkpNT6KuX1hQSQEE5CAsj5FRcXE73iIZqXjIKb/HHpPCCTyUR+fh4+P9xFa61lUEKDvk+w1T+Y3Nxcl1yUVAJICCchAeTcLAuSZrHnnSF4KMtE02ue+pkzUVEUFhbabuCXknSct29qYlkPTjWg9wNfcjwyBr1e73IhJAEkhJOQAHJeZrMZY/FZfpna6pzbMehoMf5jQtNLbwao1+sJ3TOXgY01tls1NOr6MGsj41xuZWwJICGchASQ87LejiExMRFfX1+2bdvGhg0b2Lp1K97e3sTFxdlqQUajkaysLAICAtixYwebN29m9+7dBAYGkpGRgdHoOqsBSwAJ4SQkgJyXtXktMzOTmJgYQkNDOXPmDKGhoURFRZGRkWFbjse6anZGRgbR0dGEhoYSHh5OQkKCy01KlQASwklIADk3awgVFRVRWFhoK0VFRRVGuVlrQmWfW1RU5HKTUiWAhHASEkDOr7r3YXL1ezVJAAnhJCSAhKuRABLCSUgACVcjASSEk5AAEq5GAkgIJyEBJFyNBJAQTkICSLgaCSAhnIQEkHA1EkBCOAkJIOFqJICEcBISQMLVSAAJ4SQkgISrkQASwkmcbD+AYw27SpHiMuVk+wHV/h1IAAkhhHAICSAhhBAOIQEkhBDCISSAhBBCOIQEkBBCCIeQABJCCOEQEkBCCCEc4v8BLMGA1mAGZkgAAAAASUVORK5CYII=?nolink&|Formeln}}